

Par Sylvie Jacques et Rémi Samier
Extrait de notre nouveauté Les troubles d’apprentissage en mathématiques
Les appellations et les critères pour diagnostiquer les troubles d’apprentissage en mathématiques ont beaucoup évolué ces deux dernières décennies. Aujourd’hui, le terme « troubles d’apprentissage en mathématiques » tend à remplacer le terme « dyscalculie ».
Deux classifications sont utilisées pour le diagnostic de ces troubles, le DSM-5, publié en 2013, par l’Association Américaine de Psychiatrie et la CIM-11, proposée en 2019, par l’Organisation Mondiale de la Santé.
Les points communs entre les deux classifications
Les troubles d’apprentissage en mathématiques (TAM) sont une souscatégorie des troubles des apprentissages (TA affectant la lecture, l’orthographe ou les mathématiques) qui appartiennent à la famille des troubles neurodéveloppementaux (TND).
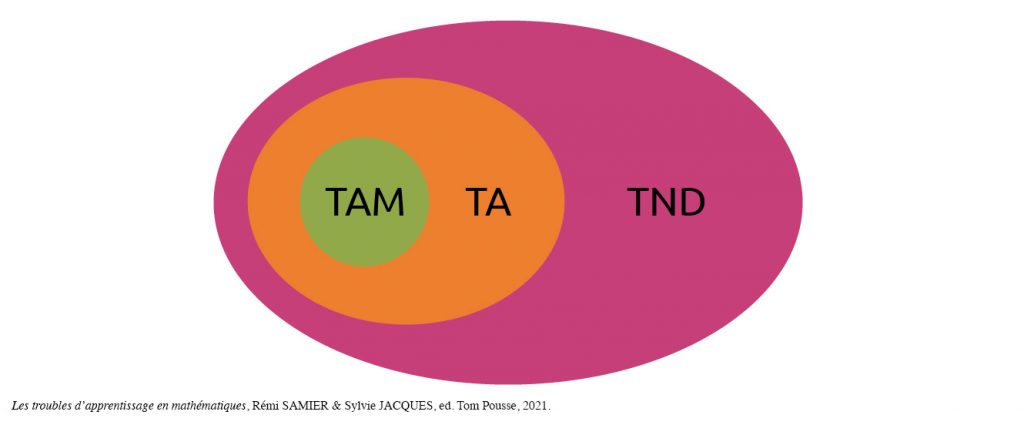
Les troubles d’apprentissage en mathématiques se caractérisent par des difficultés significatives, persistantes et handicapantes. Ils ont donc un retentissement sur la vie quotidienne (à la maison, à l’école) ou professionnelle.
Pour évoquer un trouble d’apprentissage en mathématiques, les performances en mathématiques doivent être nettement inférieures à celles attendues par rapport à l’âge de l’enfant.
Les différences entre les deux classifications
La CIM-11 précise que les performances en mathématiques peuvent être nettement inférieures par rapport au niveau de fonctionnement intellectuel.
La CIM-11 présente des critères d’exclusion. Le diagnostic de TAM ne peut pas être retenu si sont présents :
- un trouble développemental de l’intelligence ;
- une déficience sensorielle (visuelle ou auditive) ;
- une scolarisation irrégulière ;
- un défaut de maîtrise de la langue d’apprentissage ;
- des difficultés psychosociales.
Le DSM-5 explique que le TAM peut se révéler tardivement quand les stratégies de compensation de l’enfant ou de l’adolescent ont atteint leurs limites.
Le DSM-5 est plus nuancé sur les critères d’exclusion. Il mentionne que, pour poser le diagnostic de TAM, il faut que les difficultés d’apprentissage ne soient pas mieux expliquées par d’autres troubles ou par des facteurs externes, comme ceux cités précédemment pour la CIM-11.
Prévalence
La prévalence des TAM est estimée autour de 6 % des enfants d’âge scolaire.
Comorbidités / troubles associés
Les TAM sont fréquemment associés :
- aux troubles d’apprentissage de la lecture et de l’orthographe ;
- à d’autres troubles neurodéveloppementaux comme le TDAH, le trouble développemental du langage*, le trouble développemental de la coordination, etc. ;
- à des difficultés d’ordre psychologique comme les troubles anxieux.
Facteurs de risque et de protection
Pour améliorer la compréhension des troubles et de leur répercussion, la démarche diagnostique s’appuie sur la prise en compte des facteurs de risque et des facteurs de protection.
Les facteurs de protection aident à prévenir le développement ou l’aggravation d’un trouble. À l’inverse, les facteurs de risque augmentent la probabilité d’apparition d’un trouble. Ces notions de facteurs permettent de comprendre pourquoi à diagnostic identique, certains enfants s’en sortent mieux que d’autres.
Pour les TAM, plusieurs facteurs de risque ont été identifiés :
- un faible niveau socio-économique ;
- une mauvaise maîtrise de la langue d’apprentissage ;
- l’accumulation de plusieurs troubles.
Les éléments cités au sein des facteurs de risque et ceux des critères du diagnostic différentiel se recoupent. L’un des enjeux est d’apprécier par la démarche clinique si ces éléments sont des facteurs de risque ou des arguments en faveur d’un autre diagnostic.
Les signes d’alerte peuvent concerner une ou plusieurs activités mathématiques :

Lorsque des signes d’alerte sont repérés et que les difficultés persistent malgré les aides apportées, un bilan de la cognition mathématique est recommandé. Le DSM-5 précise que le diagnostic de TAM ne peut pas être posé :
- avant le début de la scolarisation ;
- sur la base d’une source unique d’informations.
Ce diagnostic clinique repose sur :
- l’histoire de la personne (ses antécédents médicaux, familiaux, son développement psychomoteur, langagier et cognitif) ;
- l’histoire des difficultés rencontrées (leurs manifestations passées et actuelles, leur retentissement sur les apprentissages et la vie quotidienne) ;
- les bulletins scolaires et les exemples de travaux scolaires qui posent problème.
Pour les situations complexes, quand un trouble sensoriel, moteur, neurologique ou une atteinte de l’efficience intellectuelle sont suspectés, la démarche diagnostique doit reposer sur un médecin expert des troubles d’apprentissage et une évaluation neuropsychologique.
Le DSM-5 précise également que le TAM persiste à l’âge adulte. Une réévaluation est donc rarement nécessaire sauf raisons spécifiques la justifiant ou sauf amélioration/aggravation des troubles.
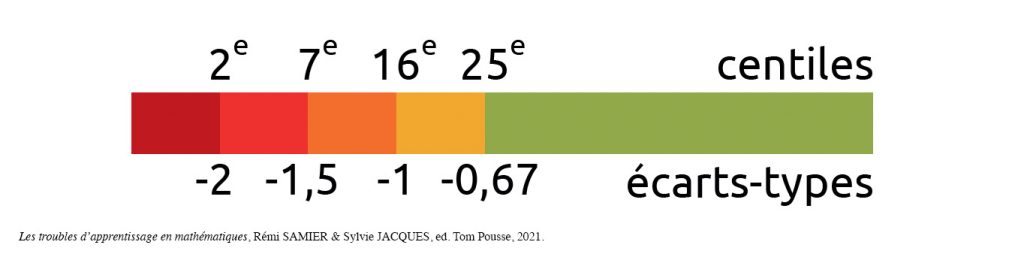
Le bilan de la cognition mathématique s’appuie sur la passation de tests normés et étalonnés. Ces tests permettent d’évaluer la performance de l’enfant afin de déterminer si l’atteinte est significative. Pour le DSM-5, des scores inférieurs à −1,5 écart-type ou au 7e centile sont nécessaires pour une grande certitude diagnostique. Cependant, des performances inférieures à −1 écart-type ou au 16e centile sont acceptées pour poser un diagnostic dans le cas où les difficultés seraient étayées par des preuves convergentes lors de l’analyse clinique.
En fonction des difficultés rapportées par le patient et son entourage (famille, enseignants, etc.), les tests permettent d’explorer différentes activités des mathématiques :
- pour objectiver le trouble ;
- pour déterminer quelles sont les fonctions cognitives défaillantes qui pourraient expliquer le trouble ;
- pour repérer quelles sont les fonctions cognitives préservées sur lesquelles s’appuyer afin de développer des stratégies de compensation.
Un bilan de la cognition mathématique teste en général :
- la cognition numérique, c’est-à-dire le sens du nombre, le code oral, le code arabe et les liens entre ces trois systèmes (accès au sens du nombre et transcodages) ;
- la compréhension de la numération ;
- la cognition arithmétique avec le calcul mental, le calcul posé et la résolution de problèmes ;
- les fonctions cognitives plus générales comme le raisonnement, le langage, les fonctions exécutives, les fonctions visuo-practo-spatiales, etc.
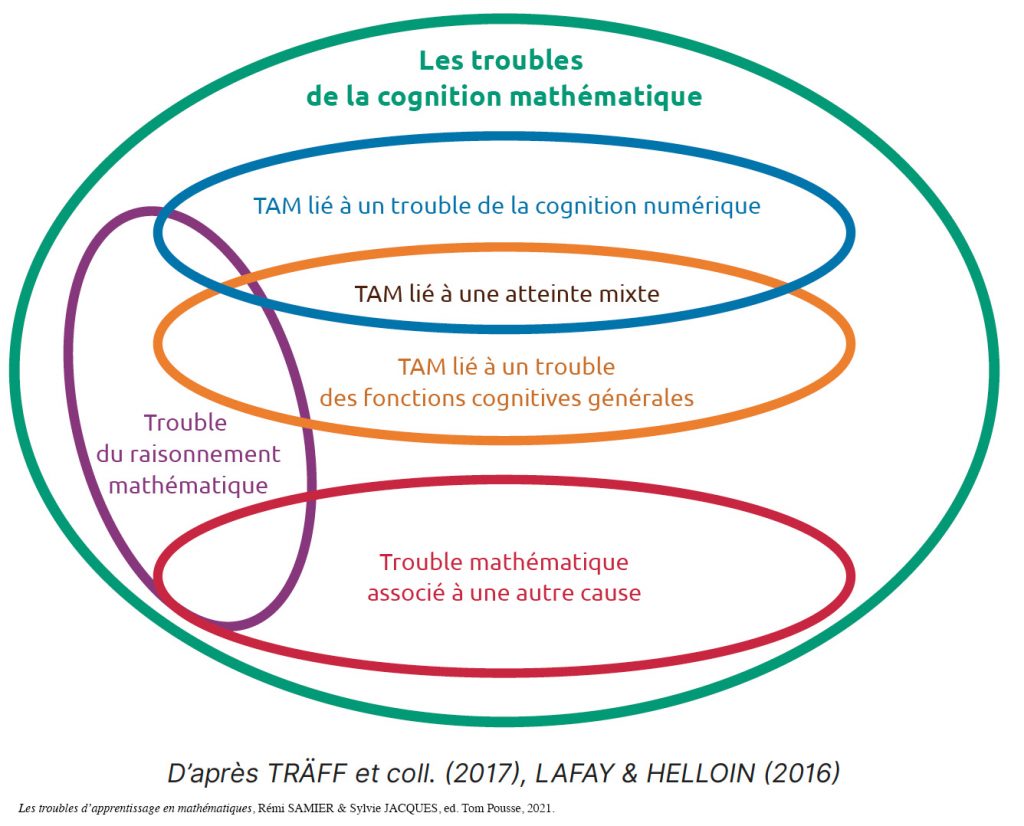
À l’issue du bilan de la cognition mathématique, il sera donc possible de déterminer s’il s’agit :
- d’un TAM (trouble d’apprentissage en mathématiques) lié à un trouble de la cognition numérique ;
- d’un TAM lié à un trouble d’une ou plusieurs fonctions cognitives générales ;
- d’un TAM lié à une atteinte mixte de la cognition numérique et de fonctions cognitives générales ;
- d’un trouble du raisonnement mathématique qui peut être associé ou non à un TAM ;
- d’un trouble mathématique associé à une autre cause identifiée (trouble du développement intellectuel, troubles sensoriels, etc.).
Ces troubles sont regroupés au sein des troubles de la cognition mathématique. L’appellation « troubles de la cognition mathématique » est un terme générique pour désigner tous les troubles mathématiques, quelle que soit la cause sous-jacente.
Avec les avancées de la recherche, les terminologies ont évolué ces dernières années. D’après les recommandations actuelles, il est préconisé de rechercher la ou les fonctions cognitives altérées en lien avec le TAM plutôt que de faire une distinction entre dyscalculie primaire et dyscalculie secondaire.

Photo by Tara Winstead from Pexels

